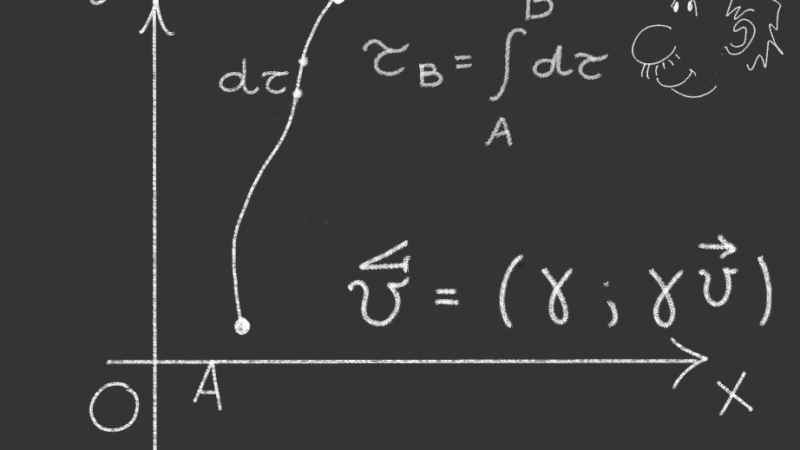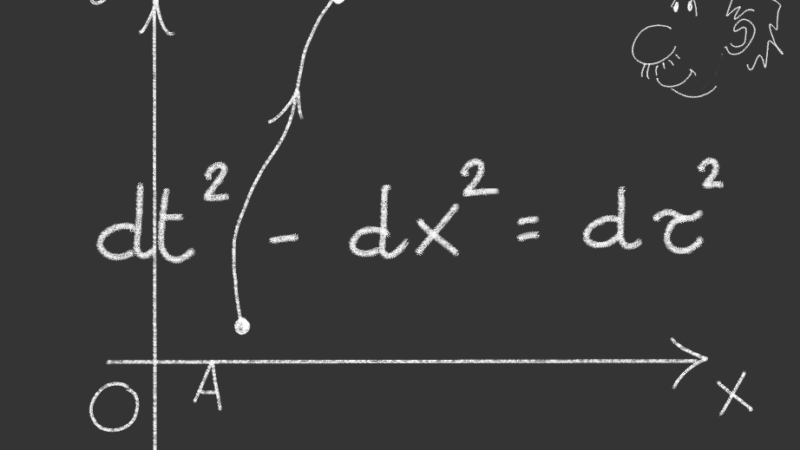7. Le trasformate di Lorentz (Parte I)

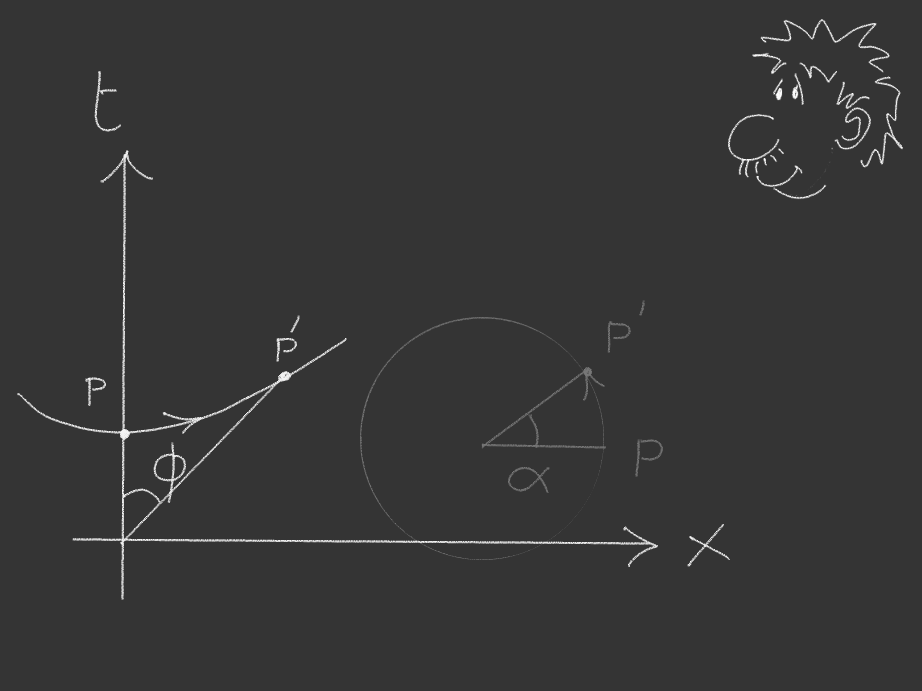
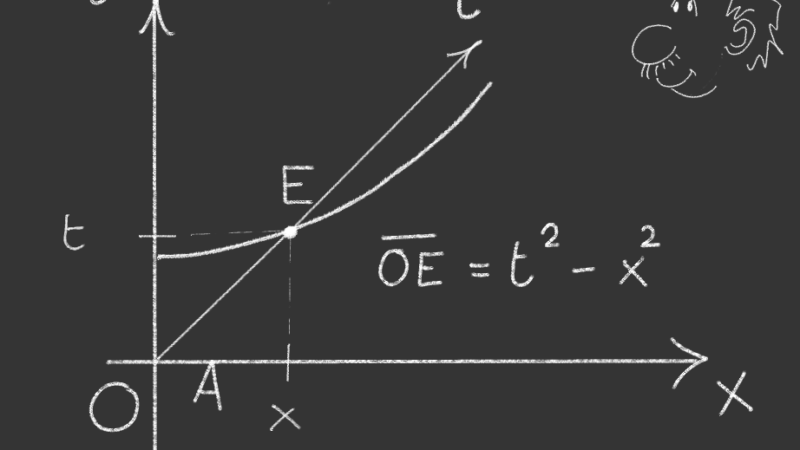
In Relatività Speciale passare da un Osservatore Inerziale ad un altro in moto con velocità v rispetto al primo, equivale ad effettuare una rotazione nello spazio-tempo. Nello spazio usuale Euclideo ruotare significa muoversi lungo un arco di circonferenza. Lo stesso vale nello spazio-tempo della Relatività (piano di Minkowski) solo che qui le circonferenze sono iperboli!

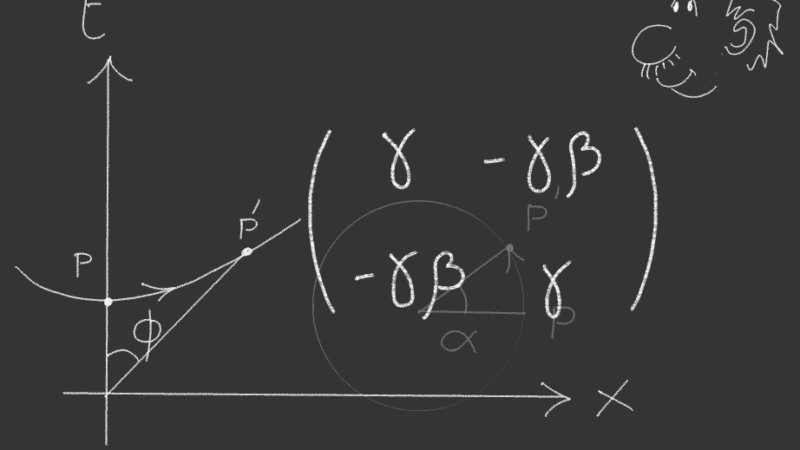
Dunque, le trasformate di Lorentz, che consentono di calcolare le grandezze fisiche di un osservatore inerziale O’ in funzione delle grandezze misurate da un altro osservatore O, altro non sono che rotazioni nello spazio-tempo!

Unisciti al Canale Telegram per essere sincronizzato con questo Blog: https://t.me/Two_Penny_Physics

Segui i video sul Canale YouTube: http://www.youtube.com/c/LorenzoGalante