Interferenza Luminosa
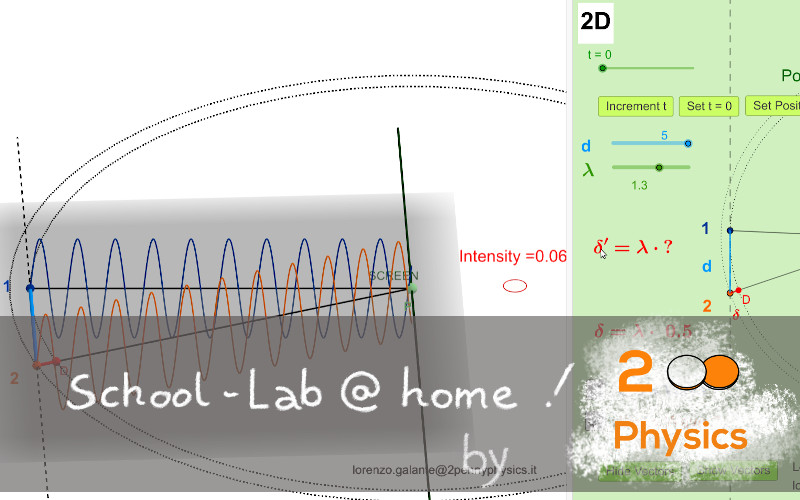
Oggi parliamo di interferenza luminosa. Ho sempre trovato non semplice spiegare in maniera soddisfacente questo fenomeno. Per questo motivo ho deciso di dedicare un po’ del mio tempo alla realizzazione di un’applicazione interattiva (su base Geogebra) che consenta di visualizzare lo spot luminoso che si vede sullo schermo nel punto in cui si incontrano due raggi di luce dello stesso colore (cioè provenienti da due sorgenti monocromatiche, p. es. due laser) .
L’applicazione, oltre a permettere di visualizzare l’intensità dello spot luminoso al variare del punto P sullo schermo, dà modo di visualizzare il modello matematico adottato in Fisica (Classica) per spiegare quel che si osserva sperimentalmente. Per mostrare come usare l’applicazione e quali siano le sue potenzialità ho preparato un video che trovate qui sotto. Se avrete la pazienza di seguirlo tutto avrete un’introduzione completa a quanto se ne può “estrarre” da un punto di vista didattico.
Per usare l’applicazione è sufficiente cliccare su questo link: Applicazione sull’Interferenza. Essa si aprirà in un’altra finestra.
Seguono tre brevi approfondimenti. Il primo sull’importanza del parametro tempo nella trattazione dell’Interferenza tra due sorgenti di luce monocromatica. Il secondo è dedicato a come condurre lo studente dalla situazione dell’app, in cui lo schermo è vicino alle sorgenti, alla configurazione alla Young con schermo all’infinito. L’ultimo riporta qualche considerazione sull’esperimento della doppia fenditura.
Qui trovi un brevissimo questionario di valutazione del post e dei materiali forniti. Se hai tempo compilalo sarà utile per valutare il lavoro svolto!
Intensità Istantanea vs Intensità Media.
Come accennato nel video iniziale, l’intensità luminosa che si osserva sperimentalmente nel punto P dello schermo non è l’intensità che appare ad un certo istante, ma la media delle intensità istantanee su un intero periodo T delle onde che si incontrano. Sulla base dell’interpretazione fisica del fenomeno (presentata nel video che descrive l’applicazione) possiamo interpretare il vettore rosso (dato dalla somma delle due onde nel punto P) come il campo elettrico istantaneo e totale in quel punto: \( \vec{E}_1 (P, t)+\vec{E}_2 (P, t) \). Come si vede bene dall’applicazione, esso ha un modulo che oscilla nel tempo, con periodo identico a quello delle onde che interferiscono. Avendo assegnato alla velocità di propagazione il valore \( c = 1\), si ha che \( T=\lambda \). Possiamo dunque esprimere il valore del campo elettrico totale in questo modo:
\( E_{tot}(P, t)\propto A \cdot sin(\frac {2\pi}{T}\cdot t) \) ,
Dove \( A \) è l’ampiezza data dal valore massimo raggiunto dal vettore rosso. L’intensità istantanea della luce va con il quadrato del campo
\(I(t) \propto E_{tot}^2(P, t) = A^2 sin^2(\frac {2\pi}{T}\cdot t) \)e l’intensità media è il valore medio su un periodo della \( I(t) \)
\( I_{Av.} = \frac{1}{T}\int_0^T A^2 sin^2(\frac {2\pi}{T}\cdot t) dt\)
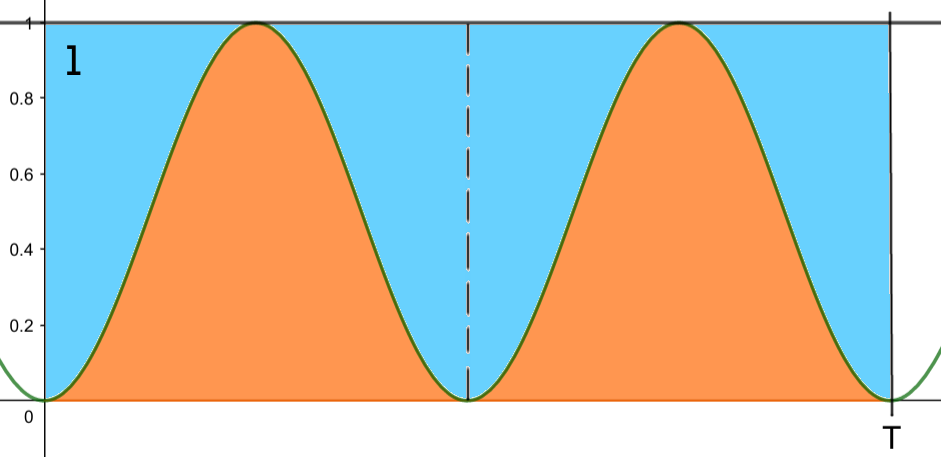
Come si può facilmente dedurre per via geometrica (vedi suggerimento fornito dall’immagine a lato) il valore medio di un seno al quadrato lungo un periodo T è pari a 1/2.
Si ha dunque: \( I_{Av.}= \frac{A^2}{2} \).
L’applicazione che trovate qui sotto è stata progettata per entrare in confidenza con il concetto di Intensità istantanea e media. Avete due onde con ugual lunghezza d’onda che si propagano lungo stessa direzione e si incontrano in un punto P su uno schermo. Muovendo lo slider \( \delta \) potete variare lo sfasamento. Con il bottone “Start Animation” potete avviare lo scorrere del tempo e godervi l’animazione. L’applicazione visualizza il vettore somma dei campi elettrici in P (vettore rosso Resultant), i vettori campo delle due onde che si sovrappongono sullo schermo (vettore 1 e vettore 2). Essa fornisce anche i valori numerici del \( E_{tot} \) (Resultant Modulus), il massimo valore di \( E_{tot} \) (Resultant Max value = A), il valore di \( I(t)\) (Instantaneous Intensity) e l’intensità media (Average Intensity).
.
Portiamo lo schermo all’infinito.
L’ Applicazione sull’Interferenza presenta i concetti fondamentali dell’interferenza della luce lavorando con due sorgenti che si incontrano in un punto P di uno schermo a distanza finita dalle sorgenti stesse. Questa, a mio modo di vedere, è la situazione da cui partire per inquadrare il fenomeno. Una volta compreso e visualizzato il significato di:
- differenza di cammino ottico,
- onda sinusoidale che si propaga in una certa direzione oscillando perpendicolarmente al cammino ottico,
- Sovrapposizione di onde in fase e in antifase,
- Interferenza costruttiva e distruttiva e suo legame con la differenza di cammino ottico,
- Intensità luminosa (istantanea e media) – (facoltativo),
ci si potrà muovere verso il caso con schermo all’infinito. Il primo passo da compiere sarà far comprendere che, se lo schermo è infinitamente lontano, possiamo considerare parallele le direzioni dei due raggi che si incontrano nel punto P. L’applicazione proposta in questa sezione (qui sotto) è di supporto alla visualizzazione/comprensione di questo fatto. Potete trascinare il punto P in alto o in basso, variare con lo slider d la distanza tra le sorgenti, impostare da tastiera il valore della distanza del punto P dalle sorgenti. Si potrà così notare che quando la distanza è di 3 ordini di grandezza maggiore della distanza d, l’occhio umano percepisce già le direzioni come parallele (d = 5, distanza = 5000).
Il tasto ‘Show Directions” offre la misura degli angoli formati dalle due direzioni con una retta orizzontale, in tal modo, volendo, si potrà quantificare il disallineamento.
Una volta accettato il parallelismo dei raggi luminosi che si incontrano in un punto di uno schermo infinitamente lontano, si può estendere la situazione presentata nell’applicazione sull’interferenza. Essa si trasforma nella situazione che vedete nell’immagine qui sotto. I colori dei vari segmenti e punti sono quelli a cui ci si è abituati usando l’applicazione, in tal modo il passaggio dovrebbe essere facilitato.
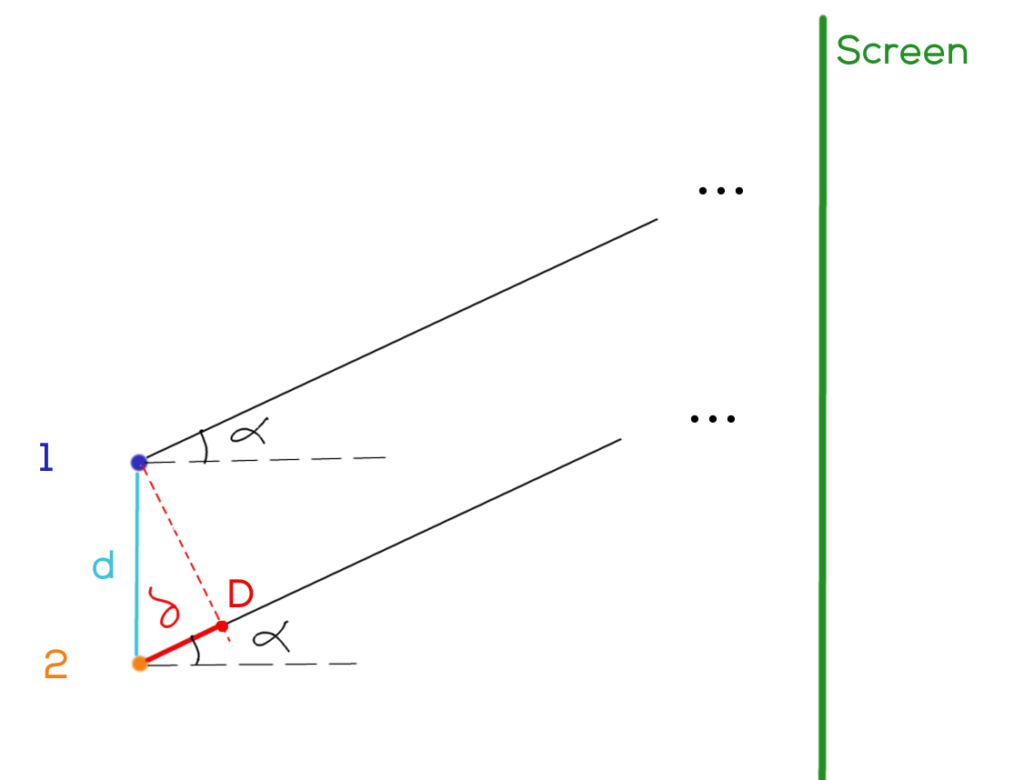
I raggi luminosi emessi dalle due sorgenti diventano paralleli, formano dunque uno stesso angolo \( \alpha \). L’arco di circonferenza centrato in P e passante per la sorgente 1, che avevamo prima, diventa il segmento perpendicolare al raggio 2 tratteggiato in rosso.
Valgono le stesse regole ricavate usando l’applicazione sull’interferenza:
- quando la differenza di cammino ottico è uguale a un numero dispari di mezze lunghezze d’onda, \( \delta=(2n+1)\cdot\frac{\lambda}{2} \), si ha interferenza distruttiva,
- quando la differenza di cammino ottico è un numero intero di lunghezze d’onda, \( \delta=n\cdot\lambda\), si ha interferenza è costruttiva.
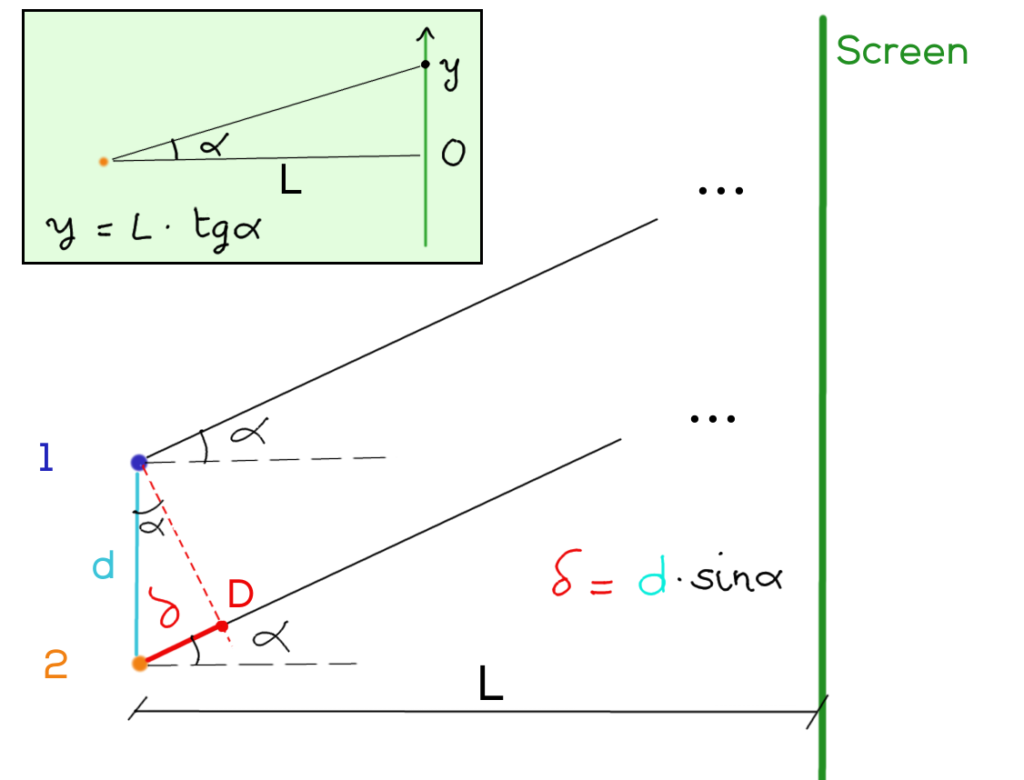
Notiamo che:
- \( \delta = d\cdot sin\,\alpha\).
- La posizione y del punto P sullo schermo (vedi box nell’immagine) è \(y=L\cdot tg\,\alpha \), (L = distanza sorgente – schermo).
- Se \( L\rightarrow\infty \), allora \(\alpha \rightarrow 0\) (lo si può sperimentare con l’app dedicata al parallelismo dei raggi) e di conseguenza \( tg\,\alpha \sim \sin\, \alpha \)
Dunque possiamo legare la condizione di interferenza costruttiva \(\delta=n\cdot\lambda\) alla posizione y dello spot luminoso corrispondente sullo schermo. Dalla condizione ricaviamo il valore di \(sin\,\alpha\) in corrispondenza del quale si verificano i massimi di intensità di luce sullo schermo:
\(\delta=n\cdot\lambda\),
\(d\,sin\,\alpha=n\cdot\lambda\quad\rightarrow\quad sin\,\alpha =\frac{n\lambda}{d}\).
Quindi esprimiamo la posizione dei massimi di intensità in funzione del valore del seno appena trovato:
\(y_{max}=L\,tg\alpha\sim L\,sin\alpha=L\cdot \frac{n\lambda}{d}\).
Il gioco è fatto! Adesso abbiamo una relazione matematica che ci consente di passare dalla distanza tra due massimi di intensità sullo schermo alla lunghezza d’onda della luce che sta interferendo (o viceversa).
Verso la doppia fenditura...
Lo studio dell’interferenza della luce risulta molto importante per poter comprendere l’esperimento della doppia fenditura.
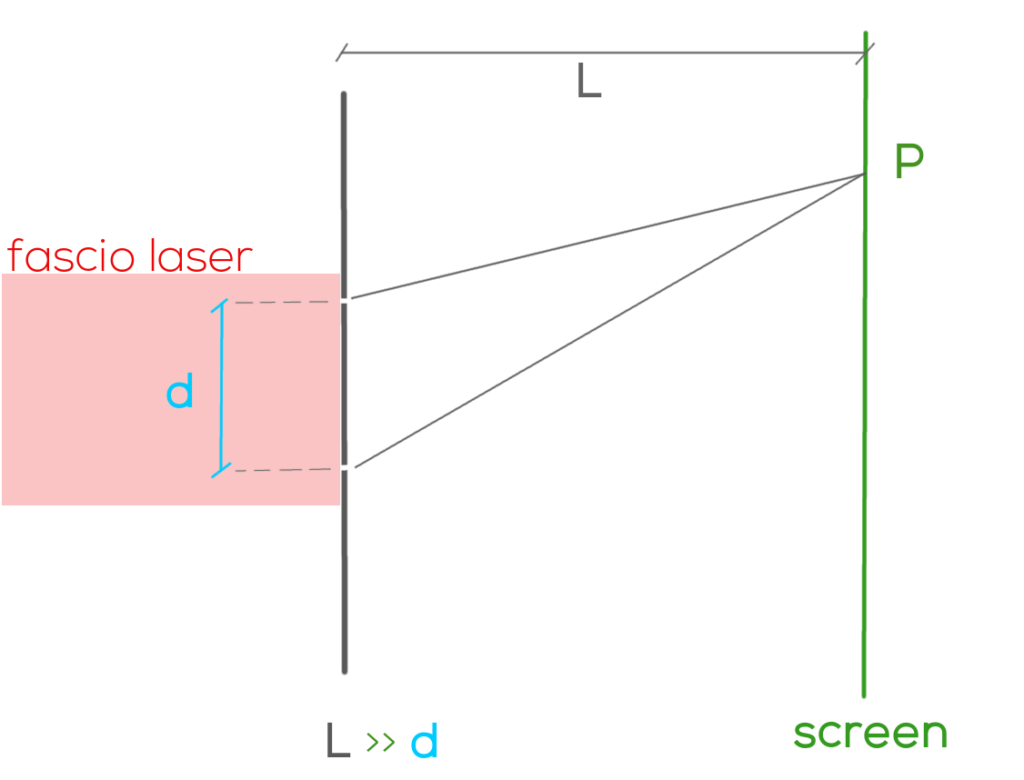
In tale contesto un fascio di luce laser viene inviato verso una doppia fenditura e la luce che attraversa la doppia “finestra” viene poi raccolta su uno schermo, solitamente posto a distanza \( L >> d \) (dove d, questa volta, rappresenta la distanza tra le due fenditure).
La connessione tra l’esperimento della doppia fenditura e l’interferenza di due raggi di luce monocromatica è dovuta alle seguenti osservazioni:
- La luce che passa attraverso la doppia fenditura interagisce con le fenditure e può essere diffusa in tutte le direzioni.
- Dalle due fenditure, dunque, emergono in continuazione raggi di luce con la stessa lunghezza d’onda che si dirigono nelle varie direzioni.
- Ciascuna fenditura si comporta dunque come una sorgente di luce monocromatica che indirizza raggi luminosi in tutte le direzioni (le sorgenti 1 e 2 che consideravamo prima studiando l’interferenza)
- Rispetto alla situazione precedentemente affrontata la differenza sta nel fatto che prima le sorgenti inviavano luce in una direzione per volta. Ora è come se esse inviassero in successione raggi in tutte le direzioni.
- Prima osservavamo uno spot luminoso in un punto P per volta, adesso su tutti i punti P dello schermo appaiono spot luminosi, gli uni al fianco degli altri, ognuno con l’intensità media che abbiamo incontrato e calcolato lavorando con una direzione per volta.
Apro un testo a caso (per l’insegnamento della Fisica nelle scuole medie superiori di II grado) e leggo che il fatto che la luce, dopo aver attraversato le due fenditure, si diriga in tutte le direzioni è spiegato utilizzando il principio di Huygens. In analogia a quanto accade alle onde che si propagano in un mezzo elastico come l’acqua.
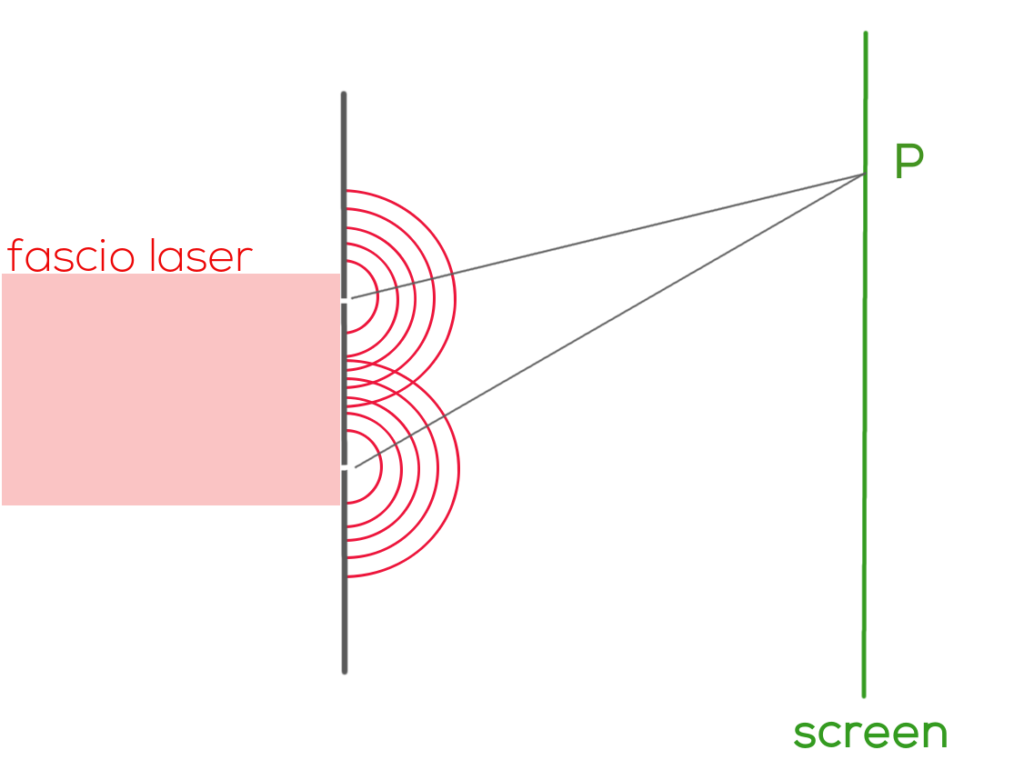
Nel caso dell’acqua abbiamo un mezzo elastico, assente nel caso della propagazione luminosa. Da un punto di vista più moderno, mi vien da dire che il destino della luce oltre le fenditure sia dovuto al sistema fisico <Luce + fenditura> e all’interazione che avviene tra le due componenti del sistema.
Ma qui si apre un discorso complesso, probabilmente ancora non risolto, che ci porterebbe alle porte della Meccanica Quantistica. Prima o poi ci arriveremo, è solo questione di tempo.