Quantità di moto in Fisica delle Particelle (2)

Come si misura la quantità di moto in Fisica delle Particelle.
Per curiosare nei labirinti della ricerca in fisica delle particelle, la prima cosa che dobbiamo fare è prendere confidenza con la misura dell’impulso \( \vec{p}\) delle particelle le cui tracce sono “fotografate” all’interno dei moderni rivelatori. Da ora in avanti non userò più il termine ‘quantità di moto’, i fisici delle particelle lo chiamano impulso o momento e lo indicano con la p minuscola.
Sì avete capito bene, state per imparare a misurare l’impulso a partire dalle tracce lasciate dalleparticelle nei rivelatori. Lo farete lavorando direttamente su veri e propri dati da un vero esperimento di fisica nucleare. Grazie ad un’applicazione interattiva appositamente progettata (la trovate più sotto), misurete l’impulso di un pione e di un nucleo di Elio che collidono. Pur non entrando in alcun dettaglio vi dico che il pione è una particella formata da 2 quark (appartiene alla categoria dei mesoni). Il nucleo di Elio è formato da 2 neutroni (n) e 2 protoni (p) [Attenzione lo stesso simbolo dell’impulso!]. L’interazione su cui lavorerete, dunque, è un’interazione che avviene a livello nucleare. Ma questo sarà la meccanica quantistica a dircelo e lo impareremo più avanti. Adesso entriamo nel vivo di questo post.
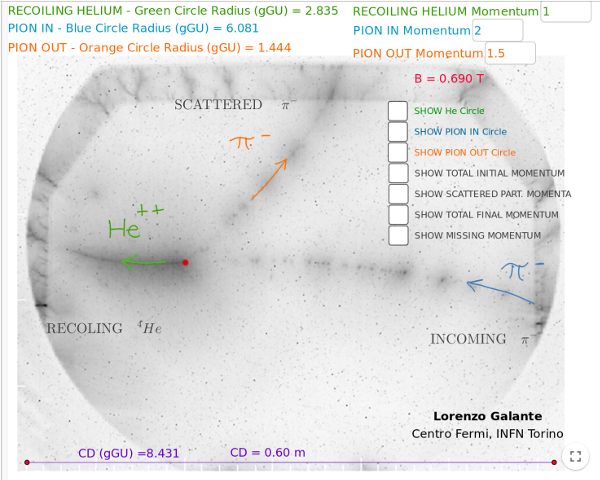
Ecco la collisione su cui lavorerete. Il pione negativo (\(\pi^-\)) entra nel rivelatore da destra (freccia blu) con un certo impulso. Si muove nel rivelatore pieno di gas d’Elio. Lo ionizza e, per questo, lascia una traccia (come fosse la scia di condensa di un aeroplano nel cielo). Nel punto indicato in rosso (Vertice di Interazione) collide con un nucleo del gas e viene deviato verso l’alto (freccia arancione). Il nucleo di Elio, colpito, rincula verso sinistra (freccia verde).
Come vedete la traccia delle particelle cariche che si sono mosse nel rivelatore è curva, molto simile a un arco di circonferenza. La curvatura della traiettoria è dovuta alla presenza di un campo magnetico costante e uniforme disposto perpendicolarmente al piano del rivelatore. In sostanza sulle particelle cariche agisce una forza di natura magnetica che ne curva le traiettorie (i dettagli matematici e la derivazione della relazioni che useremo sono presentati in questo approfondimento teorico). Il raggio r della circonferenza descritta dalle particelle cariche dipende dal loro impulso p, dall’intensità del campo magnetico B, dalla carica q della particella!
\( r=\frac{p}{qB}\)
La formula ci dice che più è alto l’impulso p, più è grande il raggio (la particella curva meno), mentre alti valori di carica e campo magnetico hanno come effetto una curvatura più intensa (r più piccolo). In poche parole vi sto dicendo che è il campo magnetico che genera la curvatura delle traiettorie che altrimenti sarebbero rettilinee. Proprio su questo fatto poggia la possibilità che i fisici hanno di determinare l’impulso delle particelle. Come vedete dalla formula scritta sopra, una volta noto il campo magnetico B, se riusciamo a misurare il raggio r degli archi di circonferenza descritti dalle particelle e se ne conosciamo la carica q, allora siamo in grado di risalire all’impulso: \( p=rqB \).
Il campo magnetico è artificialmente creato dai fisici proprio per questo motivo: la misura di p e, una volta nota la massa della particella, della sua energia E. Per l’energia avremo bisogno di un po’ di Relatività Speciale, perché come vedremo il pione che ha lasciato quella traccia stava viaggiando a circa il 90% della velocità della luce! Ma torniamo alla misura di p. Il campo magnetico B è noto (il valore lo vedete scritto in rosso, in alto a destra nella figura) ed è pari a 0.690 Tesla. La carica delle particelle la conosciamo: il pione ha la stessa carica dell’elettrone (\( q = 1.6\,10^{-19} C\)). “C” sta per Coulomb, è l’unità di misura della carica elettrica. L’Elio ha due protoni quindi la sua carica è positiva e pari al doppio di quella di un elettrone. Non ci resta che misurare i raggi delle traiettorie delle particelle che hanno interagito nella collisione e saremo in grado di calcolare il loro impulso!
Qui entra in gioco l’applicazione interattiva. Per usarla correttamente e svolgere l’attività, più sotto, trovate 3 video tutorial e del materiale riassuntivo che vi guideranno passo passo nel vostro cammino. I video sono tratti da un’analoga attività progettata per gli studenti di Fisica II del Politecnico di Torino.
Informazioni importanti sull’evento di collisione \( (\pi^-,\,He)\):
- Le tracce lasciate dalle particelle sono dovute alla ionizzazione. Cioè al fatto che esse, essendo dotate di carica, ionizzano il gas (il pione ha carica negativa, il nucleo di \( He\) ha doppia carica positiva). Le tracce di particelle neutre non sono visualizzabili da questo tipo di rivelatore!
- Le tracce di ogni particella coinvolta nell’interazione sono curve. Questo è dovuto alla Forza magnetica che agisce sulle particelle cariche in movimento.
- Il rivelatore è infatti immerso in un campo magnetico artificiale, uniforme e diretto perpendicolarmente al piano dell’immagine. L’intensità del campo \(\vec{B}\) è indicata in rosso, in alto a destra.
- Dai raggi di curvatura delle traiettorie delle particelle cariche è possibile risalire al loro impulso \( \vec{p}\) (Questo concetto è spiegato in dettaglio nell’approfondimento teorico).
Questa breve panoramica dovrebbe essere sufficiente a comprendere alcuni concetti fondamentali nella ricerca in Fisica Nucleare e delle Particelle:
- I rivelatori di particelle sono spesso immersi in un intenso campo magnetico artificiale \( \vec{B}\).
- Il campo magnetico è introdotto con il preciso scopo di curvare le traiettorie delle particelle cariche (cioè introdurre un raggio di curvatura r).
- Una volta nota la carica della particella, il raggio di curvatura indotto dal campo magnetico consente di risalire all’impulso p della particella.
SCOPO DELL’ATTIVITÀ.
In sostanza dovrete usare l’applicazione per:
- Valutare i raggi di curvatura delle 3 tracce presenti nell’evento di collisione.
- A partire dai valori dei raggi calcolare l’impulso delle 3 particelle in unità di 108 eV/c.
- Visualizzare sull’immagine dell’evento i vettori impulso prima e dopo l’interazione.
- Verificare se la legge di conservazione della quantità di moto sia valida anche su scale nucleari e sub-nucleari
I tutorial e gli approfondimenti che seguono vi guideranno in questa attività.
Video Tutorial 1: come misurare il raggio di curvatura delle tracce del pione e dell’He.
Video Tutorial 2: come si calcola l’impulso \( \vec{p}\) a partire dal raggio di curvatura misurato.
Video Turorial 3: conversione alle unità di misura adottate in fisica delle particelle (\( \frac{eV}{c}\)) e visualizzazione dei vettori impulso dell’evento di collisione \( (\pi^-,\,He)\)‘.
Se qualcosa non funziona mentre usi l’applicazione, aggiorna la pagina.

Attenzione alla parete laterale del rivelatore. Come puoi vedere nell’immagine, la parte della traccia del pione uscente nel riquadro verde non è da considerare. E’ una ionizzazione avvenuta sulla parete laterale della camera del rivelatore.
Unisciti al Canale Telegram per essere sincronizzato con questo Blog: https://t.me/Two_Penny_Physics
Segui i video sul Canale YouTube: http://www.youtube.com/c/LorenzoGalante